

# The rotation takes place in the other two dimensions. The form of the rotated component is similar to the radial vector in 2D planar polar coordinates (r, ) in the Cartesian basis where ex, ey are unit vectors in their indicated directions. # The rotational axis is the dimension into which `v` is pointing.įixed_dim = ] It is more concise and more efficient (on my machine), though it still doesn't feel "canonical" in the way I was hoping for. Now I just need a way to combine that with the 2D rotation matrix somehow.ĮDIT: After iterating a bit with ChatGPT4, I ended up with the following code. What I have tried so far: If I take the outer product np.outer(v, v) I get a 3-by-3 matrix that is the identity for my fixed dimension. (I'm assuming we're in the standard Cartesian coordinate system with dimensions x, y, z. For the sake of exmaple, lets say we keep y fixed. Now I want to apply that same rotation to a 3D vector, keeping 1 chosen dimension fixed. def rotation_matrix(move):įixed_dim = 0 if v else 1 if v else 2 will rotate a 2D vector v by 90 degrees clockwise when I take the matrix-vector product Mv. I encode a move as a pair (v, d), where v is the vector (ranging over all v in ^3 with 1-norm equal to 1), and d is the "direction" (1 for clockwise, -1 for counterclockwise). It works by computing M' from M similarly to the way I described above, but this feels rather ad-hoc and tedious.Ĭan I express this more elegantly in terms of standard linear algebra operations instead? I'm looking for concise, beautiful code.ĭetails: In my code, a "move" is any 90 degree rotation (clockwise or counterclockwise) of some "slice" (hyperplane) pointed to by a standard unit vector or its opposite.
#ROTATE VECTOR 2D CODE#
I have code for computing M' in Python, shown below.
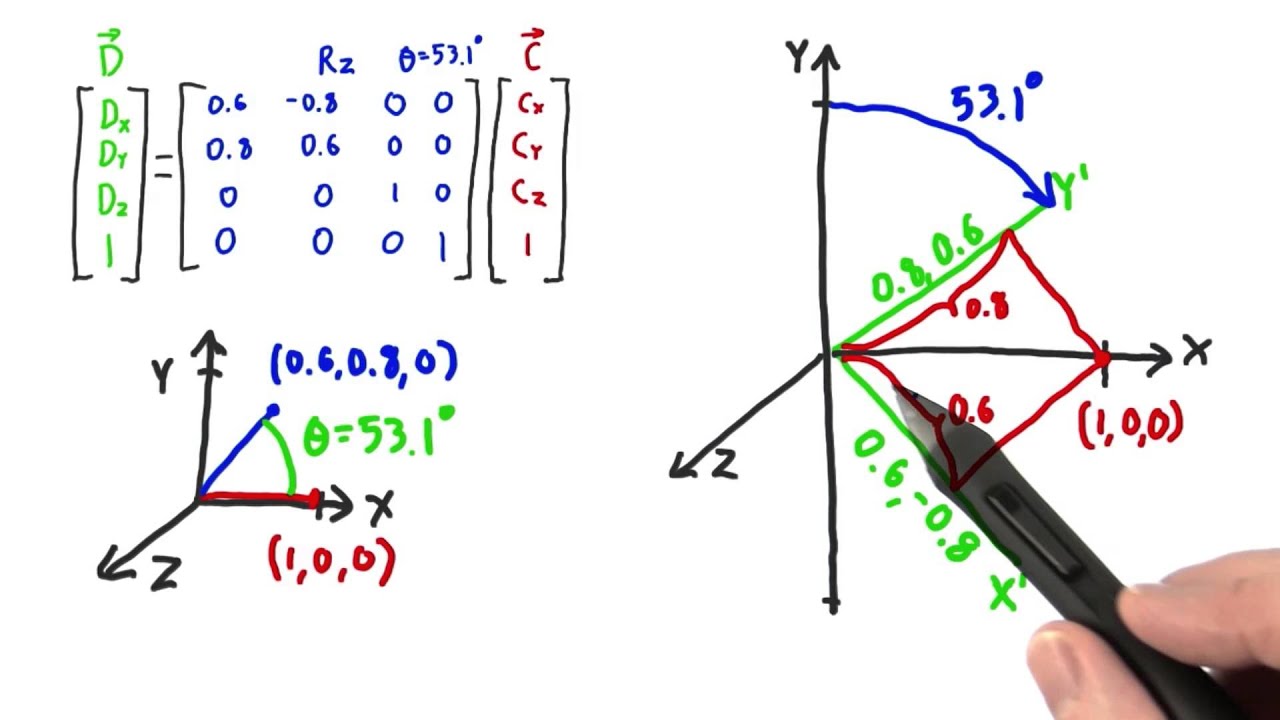
To do that, I can construct sort of a mix M' of the 3D identity matrix and my rotation matrix M, where I take M, add the extra dimension y by adding zeros to M, and then set M' = 1 so M' is the identity in the y dimension. (I'm assuming we're in the standard Cartesian coordinate system with dimensions x, y, z.)
Will rotate a 2D vector v by 90 degrees clockwise when I take the matrix-vector product Mv. From linear algebra, I know that the matrix


 0 kommentar(er)
0 kommentar(er)
